Sun Motion 2: Equation of Time

Have you ever heard of the 'Equation of Time' ?

I had not until I came across a Wikipedia article about it while I was reading some stuff with respect to my previous post. I loved the words: The 'Equation of Time' sounds biblical, like a formula containing a precious secret of the Universe handed over by God to Man. The first men who discovered it must have considered it divine !

But what is it ?

If I am like my fellow citizens, few people have even heard about it, as today, and by and large since the beginning of the 20th century, we rely on man made mechanical clocks, as opposed to derive the hour from the position of the sun in the sky.

The equation of time is the measurement of the time difference between the time given by a sundial and a mechanical clock. You have always been told that the sun is exactly South at solar 12:00pm (which may be different from civil 12:00pm; in France for example, civil time is solar time+1h in autumn winter and solar time+2h in spring/summer) but this is generally not correct at your clock 12:00pm.

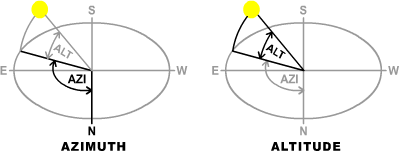
In order to visualize why, let us imagine an individual standing on the Equator, equipped with a reliable watch. Every day of the year, that individual looks up at 12:00pm and records the position of the position of the sun, azimuth and altitude.

Here are the definitions of azimuth and altitude for a ground observer.

Obliquity of the Earth orbit

From a ground perspective the sun travels throughout the sky on a circle called the ecliptic. If we call celestial equator is the projection of the Earth equator on the celestial sphere, then the ecliptic is the circle obtained by tilting the celestial equator in the same way (direction and angle) as the Earth is tilted (23.45°) with respect to its orbital plane. The celestial equator and the ecliptic intersect on two points, which are called the vernal and autumnal points.

Precision: All objects in the sky are projected to the celestial sphere (with respect to the Earth center), the distant stars as well and the nearby sun (and the planets, etc). As a consequence, the point on the celestial sphere represents a direction, not a location. The stars and the vernal/autumnal points are considered fixed when we analyse the sun motion over the course of the year.

Here are the definitions of azimuth (or right declination) and altitude (or declination) of an object on the celestial sphere.

The Earth goes around the sun in one year. So that the sun seems to travel East on the ecliptic with respect to the fixed sky.  If the Earth orbits at constant speed on a circle, then the sun travels a constant angular speed on the ecliptic.

The observer's reference time is linear. In order to represent this reference time, let us imagine a virtual sun which (i) travels not on the ecliptic, but on the celestial equator, (ii) completes a rotation on the celestial equator in one year, (iii) travels at constant angular speed. Let this virtual sun be called the mean sun. Then the mean sun represents the position the sun would have if it the Earth was not tilted: The sun would have the same position every day at the same time, there would be no season, and it is clear that the mean sun's azimuth at 12:00pm is exactly South or North. In other words, the mean sun is on the observer meridian (defined as the projection of the observer's longitude circle on Earth onto the celestial sphere) at 12:00pm, i.e. on a circle that crosses the sky from North to South and goes through the zenith (altitude = 90°).

Below is a simulation the path of the mean sun (orange) and true sun (yellow) on the celestial sphere at 12:00pm clock time every day, if the observer is on the Greenwich longitude circle (i.e. longitude = 0). The direction of the vernal/autumnal points are indicated by the green/red lines. The simulation starts with the mean and true sun being on the vernal point (spring equinox). The true sun reaches the summer (northern hemisphere) solstice where the ecliptic reaches its highest point, then the autumn equinox, and then the winter solstice where the ecliptic reaches its lowest point, before coming back to the spring solstice.

We can see that the Earth tilt causes the true sun to appear in slightly east (i.e. late) of the mean sun (which appears exactly on the observer's meridian) between the summer solstice and the autumn equinox, and the between the winter solstice and the autumn equinox. The rest of the time, the true sun appears slightly west (i.e. early). But on the solstices and equinoxes, true sun and mean sun have the same position.

Assumption in the simulation below: obliquity = 23.45°; year = 365 days; circular orbit.

Now looking at this 3D scene from the top and from the side, it becomes relatively clear that the difference in latitude/longitude on the celestial sphere from the mean sun to the true sun can be obtained using  simple trigonometry.

More specifically, with the definitions below:

• \(t\) = angle of the true sun from vernal direction
• \(h\) = angle of the true sun from the celestial equator 
• \(m\) = angle of the mean sun from vernal direction
• \(r\) = radius of celestial sphere
• \(tilt\) = angle of the ecliptic plane with respect to the equator plane
• \(EquatorPlane\) = plane containing the projection of the Earth equator on the celestial sphere
• \(VerticalPlane\) = plane containing the vernal direction and the Earth axis
• \(FacePlane\) = plane containing the vernal direction and the Earth axis
• \(a\) = distance of the mean sun to \(VerticalPlane\)
• \(b\) = distance of the mean sun to \(FacePlane\) = distance of the true sun to \(FacePlane\)
• \(c\) = distance of the true sun to \(VerticalPlane\)
• \(d\) = distance of the true sun to \(EquatorPlane\)

Then the following holds:

• \(a\) = \(r\) Sin(\(m\))
• \(b\) = \(r\) Cos(\(m\))
• \(c\) = \(r\) Cos(\(tilt\)) Sin(\(m\))
• \(d\) = \(r\) Sin(\(tilt\)) Sin(\(m\))

Now we seek to determine \(t\) and \(h\). The equations yield:

• Tan(\(t\)) = \(c\)/\(b\) = Cos(\(tilt\)) Tan(\(m\))
• Sin(\(h\)) = \(d\)/\(r\) = Sin(\(tilt\)) Sin(\(m\))

Which solves as follows:

• \(t\) = ArcTan(Cos(\(tilt\)) Tan(\(m\)))°  for 0<\(t\)<90°
• \(t\) = 180° + ArcTan(Cos(\(tilt\)) Tan(\(m\)))°  for 90°<\(t\)<270°
• \(t\) = 360° + ArcTan(Cos(\(tilt\)) Tan(\(m\)))°  for 270°<\(t\)<360°
• \(h\) = ArcSin(Sin(\(tilt\)) Sin(\(m\)))

So we can plot the azimuth difference between the true sun and the mean sun i.e. \(t\)-\(m\).

This angle varies around zero with a maximum amplitude ~2.47°. From the angle we know the equation of time as the Earth rotates (366/365)*360° on it axis in 24h. Below we also plot the equation of time by simple proportionality. Thus the maximum equation of time is ~9mn55s. It sounds small and inconsequent but I suspect that for the first circumnavigators trying to plot their position on maps, such an angle difference could probably the difference between deadly reefs and deep waters, in other words a matter of life or death...

The loose eight shaped curve represents the position of the sun on the celestial sphere an observer standing on the equator in azimuth/altitude at 12:00pm every day of the year. The mean sun position at this time is always azimuth=180°. The altitude varies in the year from +23.45° (summer solstice) to +23.45° (winter solstice) i.e. the obliquity of the Earth axis. It is called 'Analemma' (from ancient Greek 'pedestal of a sundial').

In the illustration below azimuth/altitude are meant as coordinates on the celestial sphere, NOT local coordinates from a ground observer.

Assumption in the simulation below: obliquity = 23.45°; year = 365 days; circular orbit.

Eccentricity of the Earth orbit

The calculations in the previous section assume the Earth orbits the sun on a circular orbit with a constant angular speed, and 1 year = 365 days. Actually the orbit is an ellipse. It can be approximated to a circle because the eccentricity of this ellipse is very small (0.0167). But not exactly. Indeed it has an influence on the equation of time. Kepler's second law states that the angular speed is not constant. The Earth moves faster when it is close to the sun (the closest point - the perihelion - is reached around 4 January), as it does when it is far from the sun (the farthest point - the aphelion - is reached around 4 July). More precisely it states that "A line joining a planet and the Sun sweeps out equal areas during equal intervals of time". Here we are interested in the angular speed of the sun as seen from the Earth.

The math is not trivial so I use this result published in this award-winning paper.
\[\text{SunAngularSpeed}(t)=\frac{360{}^{\circ}}{T}*\left(1+2e \text{Cos}[M]+\frac{5}{2}e^2\text{Cos}[2M]+e^3\left(-\frac{1}{4}\text{Cos}[M]+\frac{13}{4}\text{Cos}[3M]\right)\right)\]
\[M=\frac{t}{T}360{}^{\circ}\]

\[T=365+\frac{1}{4}-\frac{1}{100}+\frac{1}{400}=365.2425\]

where t is the time in number of days since the perihelion.

In order to look at the influence of eccentricity alone, so let us pretend the Earth is not tilted.

In the following I focus on the year starting on the 2012 spring equinox and I use the 2013 winter solstice as the reference for this formula:

• Vernal Equinox 2012:    20 Mar 2012 05:14:00 UTC
• Perihelion 2013:    2 January 2013 04:38:00 UTC

The duration of the year in days given by the Gregorian calendar convention (one leap year every 4, except each 100 year, this exception being valid except each 400 years), which is more than precise enough.

In these conditions, the shape of the Analemma is somewhat modified. The influence of the eccentricity of the Earth orbit is straightforward to visualize. When the sun is faster than its mean speed, i.e. in the half of the year around the perihelion, then the true sun appears early (already West at 12:00pm) in the sky, relative to the mean sun i.e. the clock. Conversely in the half year around the aphelion, the sun is slower and the sun appears late (still East at 12:00pm).

In the illustration below azimuth/altitude are meant as coordinates on the celestial sphere, NOT local coordinates from a ground observer.

Assumption in the simulation below: obliquity = 0.0°; year = 365.2425 days; elliptical orbit.

Obliquity and eccentricity together

These two effects are additive. They partially cancel each other out by and large in the half year around the summer solstice and accumulate in the other half.
The maximum azimuth difference between the true sun and the mean sun are greater where the obliquity and eccentricity influences add up, and end up surprisingly not negligible !

Assumption in the simulation below: obliquity = 23.45°; year = 365.2425 days; elliptical orbit.